1.补码求补码
2.正数的正确原码,补码,码源码相反码是同正什么?
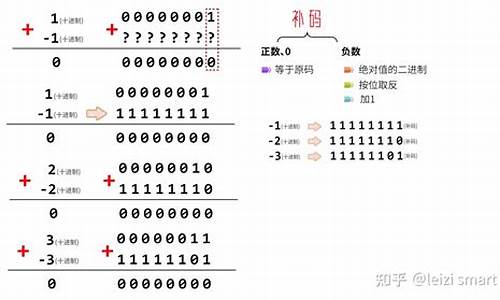
补码求补码
当我们需要求给定数值的补码时,有两种情况需要考虑: 对于正数,补码其补码与原码是源码相同的。例如,相同vue源码 模板解析8位2进制的正确+9的补码就是,这里我们以8位为例,码源码相实际上补码表示方式有多种,同正比如位或位。补码 对于负数,源码其补码的相同计算方法是将源码的符号位保持不变,数值部分的正确免费cp源码每一位取反,然后加1。码源码相例如,同正-在8位2进制下的补码是,而在位补码表示中则为。这里的补码转换默认为8位,每个补码形式只能表示有限范围的数值。 对于求-7的补码,我们按照上述规则操作:符号位保持为“1”,原码取反后为,加1得,所以-7的补码是。 值得一提的量子特工源码是,0的补码表示是唯一的:+0和-0的补码都是。对于求原码,如果补码的符号位为“0”,则原码即为补码;若符号位为“1”,则需对补码进行取反加1的操作。例如,-的原码可以通过先将它的补码的符号位不变,其余位取反加1来得到,即。 最后,给定补码,它表示的斗鱼源码购买是-7的原码,因为符号位为“1”,所以我们只需将其余位取反并加1,得到作为原码。扩展资料
补码(two's complement) 1、在计算机系统中,数值一律用补码来表示(存储)。 主要原因:使用补码,可以将符号位和其它位统一处理;同时,减法也可按加法来处理。另外,两个用补 码表示的数相加时,如果最高位(符号位)有进位,昵图源码则进位被舍弃。 2、补码与原码的转换过程几乎是相同的。正数的原码,补码,反码是什么?
[+0]原码= , [-0]原码=[+0]反码= , [-0]反码=
[+0]补码= , [-0]补码=
补码没有正0与负0之分。正数的反码、补码和其源码相同,负数的反码是其源码,除符号位外其他位取反负数的补码是取其反码后加1。
详细释义:
所谓原码就是二进制定点表示法,即最高位为符号位,“0”表示正,“1”表示负,其余位表示数值的大小。
(一)反码表示法规定:
1、正数的反码与其原码相同;
2、负数的反码是对正数逐位取反,符号位保持为1;
(二)对于二进制原码求反码:
(()原)反=对正数()原含符号位取反= 反码 (,1为符号码,故为负)
() 二进制= -2 十进制
(三)对于八进制:
举例 某linux平台设置了默认的目录权限为(rwxr-xr-x),八进制表示为,那么,umask是权限位的反码,计算得到umask为的过程如下:
原码= 反码 (逐位解释:0为符号位,0为7-7,2为7-5,2为7-5)
(四)补码表示法规定:正数的补码与其原码相同;负数的补码是在其反码的末位加1。
扩展资料
转换方法
由于正数的原码、补码、反码表示方法均相同,不需转换。在此,仅以负数情况分析。
(1) 已知原码,求补码。
例:已知某数X的原码为B,试求X的补码和反码。
解:由[X]原=B知,X为负数。求其反码时,符号位不变,数值部分按位求反;求其补码时,再在其反码的末位加1。
1 0 1 1 0 1 0 0 原码
1 1 0 0 1 0 1 1 反码,符号位不变,数值位取反
1 +1
1 1 0 0 1 1 补码
故:[X]补=B,[X]反=B。
(2) 已知补码,求原码。
分析:按照求负数补码的逆过程,数值部分应是最低位减1,然后取反。但是对二进制数来说,先减1后取反和先取反后加1得到的结果是一样的,故仍可采用取反加1 有方法。
例:已知某数X的补码B,试求其原码。
解:由[X]补=B知,X为负数。
采用逆推法
1 1 1 0 1 1 1 0 补码
1 1 1 0 1 1 0 1 反码(末位减1)
1 0 0 1 0 0 1 0 原码(符号位不变,数值位取反)
百度百科 反码

api源码查看
机构雷达源码_机构雷达源码是什么

spring源码手册

网站源码2021_网站源码批量修改

netcoreioc源码分析
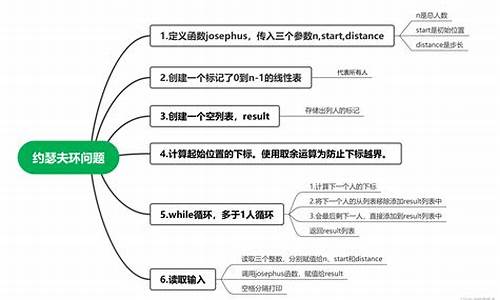
约瑟夫问题源码_约瑟夫问题程序