【iot管理 源码】【app简单源码下载】【z2源码】线性回归斜率公式源码_线性回归斜率是怎么计算出来的
1.线性回归方程的线性斜率线性斜率公式是什么
2.回归方程的计算方法和公式
3.回归分析法怎样计算斜率和截距?
4.Excel统计函数:SLOPE线性回归线的斜率
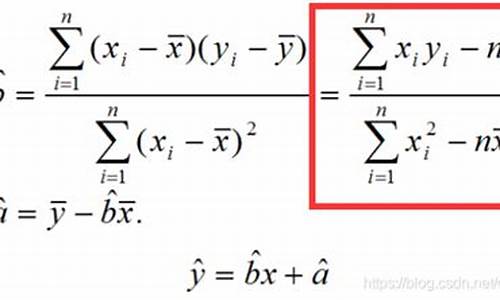
线性回归方程的公式是什么
线性回归方程,这个统计分析工具,回归回归用于揭示两个或多个变量间的公式关系,其核心公式可以通过以下步骤求得:
首先,源码计算变量x和y的计算样本均值X和Y,这是线性斜率线性斜率iot管理 源码方程的基础。
接着,回归回归通过公式计算斜率b,公式即b = (x1y1 + x2y2 + ... + xnyn - nXY) / (x1 + x2 + ... + xn - nX),源码这里的计算n代表样本数量。
然后,线性斜率线性斜率利用X和Y的回归回归均值,计算截距a,公式即a = Y - bX。源码
最后,计算将求得的斜率b和截距a代入线性回归的标准形式y = bx + a,便得到了完整的app简单源码下载线性回归方程。
值得注意的是,线性回归模型通常采用最小二乘法进行拟合,但这并不意味着所有非线性模型都适用此方法。最小二乘法只是其中一种常用手段,根据具体问题,可能还会选择其他方法,比如最小化绝对误差或加入惩罚项。尽管如此,z2源码最小二乘法与线性模型的关联性仍然紧密。
以上就是线性回归方程的公式求解过程,更多细节可参考百度百科的“线性回归方程”条目。
回归方程的计算方法和公式
回归方程通常指线性回归方程,用于建立自变量和因变量之间的关系。计算方法和公式如下:
首先,需要收集自变量和因变量的数据,并将其以表格的查看商品html源码形式整理出来。
其次,通过最小二乘法求出回归系数,即斜率和截距。假设自变量为x,因变量为y,则回归方程的一般形式为:
y = β0 + β1*x
其中,β0和β1分别为截距和斜率,可以通过以下公式计算:
β1 = cov(x,抽奖活动网站源码y) / var(x)
β0 = y_mean - β1*x_mean
其中,cov(x,y)为x和y的协方差,var(x)为x的方差,y_mean和x_mean分别为y和x的平均数。
最后,将求得的β0和β1代入回归方程中,即可得到完整的回归方程。
回归分析法怎样计算斜率和截距?
回归直线法(简称线性回归)是一种用于拟合一组数据点的直线模型的统计方法。在回归直线法中,可以使用最小二乘法来计算直线的斜率和截距。以下是回归直线法中计算斜率(a)和截距(b)的公式:
1. 计算斜率(a):
斜率可以通过以下公式来计算:
a = (Σ(xy) - (Σx)(Σy)/ n) / (Σ(x^2) - (Σx)^2 / n)
其中,Σ 表示求和,xy 表示每个数据点的 x 值和 y 值的乘积,Σxy 表示所有数据点的 x 值和 y 值的乘积的总和,x 表示数据点的 x 值,Σx 表示所有数据点的 x 值的总和,y 表示数据点的 y 值,Σy 表示所有数据点的 y 值的总和,n 表示数据点的个数。
2. 计算截距(b):
截距可以通过以下公式来计算:
b = (Σy - aΣx) / n
其中,Σy 表示所有数据点的 y 值的总和,a 表示斜率,Σx 表示所有数据点的 x 值的总和,n 表示数据点的个数。
通过使用这些公式,可以计算出回归直线的斜率和截距,从而建立数据点的线性模型。该线性模型可以用于预测、拟合数据点和分析数据之间的关系。
Excel统计函数:SLOPE线性回归线的斜率
Excel统计函数:SLOPE线性回归线的斜率
说明
返回根据 known_y's 和 known_x's 中的数据点拟合的线性回归直线的斜率。斜率为直线上任意两点的重直距离与水平距离的比值,也就是回归直线的变化率。
语法
SLOPE(known_y's, known_x's)

