1.二级C语言等级考试该怎样自学啊
2.在六西格玛中提到了"关键的约瑟少数".
3.用c语言实现约瑟夫环
4.C语言-有趣的约瑟夫问题及解决办法

二级C语言等级考试该怎样自学啊

       C语言二级必然是已经涉及了一些数据结构和算法设计,想自学可以买一本谭浩强的数据结构初讲，清华大学出版社，夫问然后就是题源花一些时间多找些程序看看，最好是码约一些经典的编程题，例如：八皇后，问题约瑟夫问题，程序replace函数源码实现骑士遍历问题和二叉树问题，约瑟都非常具有代表性。夫问建议从网上找一些源代码下下来看看，题源有不小的码约帮助，还有就是问题要多花些时间自己练习，不然遇到程序还是程序afsim仿真源码不会写。

在六西格玛中提到了"关键的约瑟少数".

       “关键的少数和次要的多数”的关系就是/法则，又称为帕累托法则，夫问即指%的题源事态成因，可以导致%的事态结果。当然，/并不是精确的关系，而是方便的比喻

       帕累托因对意大利%的人口拥有%的财产的观察而著名，后来被约瑟夫·朱兰和其他人概括为帕累托法则（/法则），后来进一步概括为帕累托分布的概念。

       帕雷托法则（Pareto principle），也称为/法则，源码前端费用此法则指在众多现象中，%的结果取决于%的原因，而这一法则在很多方面被广泛的应用。如%的劳动成果取决于%的前期努力、%的人做了%的工作或者%的维基人贡献了%的维基条目等等。但也常常被滥用、误用，例如解决一个问题符合/法则，因为%的问题由%的资源来解决。

       这个法则最初是意大利经济学家维弗雷多·帕雷托（Vilfredo Pareto）在年对意大利%的人口拥有%的财产的观察而得出的，后来管理学思想家约瑟夫·朱兰（Joseph M. Juran）和其他人把它概括为帕雷托法则。西瓜编程源码

       若进一步推算，以掌握了%财富的人作统计，会发现4%的人口(% × %)掌握了社会%(% × %)的财富。这一猜想说明绝大部分的产量或结果取决于一小部分的投入和劳动。在商业活动中，%的销量来自与%的客户。管理者利用这种猜想制定商业决策，虽然很多时大致符合结果，但仍待进一步证实。

       帕雷托法则是更广泛现象帕雷托分布的特例。假如在帕雷托分布中选择合适的配方管理源码变量，不仅一个%的影响由%的原因所造成，%里的前%影响也是由%的前%原因所造成 （%的%是%，%的%是4%，意味着这是/4法则）。

       帕雷托法则与帕雷托最优（Pareto efficiency）无关，虽然也是维弗雷多·帕雷托提出的。

       帕雷托法则在品质控制上有很多的应用，它是全面品质管理、六标准差(Six Sigma)的关键工具，此外，也是Pareto chart的基础。

       在计算机科学里，帕雷托法则可借由观察%的资源是由%所操作使用，来最佳化资源。在软件工程上，常有接近%的电脑程式执行次数花费在%的程式源代码执行。在图书资讯学里，一间图书馆的%馆藏是由%的读者所借阅。

       帕雷托法则被当做ABC-analysis和XYZ-analysis的基准线，广泛的使用在进行物流和采购时，以达成最佳化商品进货(维持进货的花费)的目的。

用c语言实现约瑟夫环

       正好之前写过基础的约瑟夫环，稍作修改就可以满足你的题目

#include <stdio.h>

       #include <stdlib.h>

       typedef struct _node {

           int id;

           int key;

           struct _node *next;

       } Linklist;

       int main() {

        int n, m;

        scanf("%d %d", &n, &m);

        int i, count = 0;

        Linklist *head = (Linklist*)malloc(sizeof(Linklist)), *tail = head;

        head->id = 1;

        scanf("%d", &head->key);

        head->next = head;

        for(i = 2; i <= n; i++) {

        Linklist *p = (Linklist*)malloc(sizeof(Linklist));

        p->id = i;

        scanf("%d", &p->key);

        p->next = head;

        tail->next = p;

        tail = p;

        }

        while(head != tail) {

        if(++count % m) {

        tail = head;

        } else {

            m = head->key;

            count = 0;

        printf("%d ", head->id);

        tail->next = head->next;

        free(head);

        }

        head = tail->next;

        }

        printf("%d\n", head->id);

        free(head);

        return 0;

       }

C语言-有趣的约瑟夫问题及解决办法

       约瑟夫问题，亦称约瑟夫置换，是计算机科学和数学中的一个经典问题。它来源于一个关于历史学家约瑟夫的故事，故事讲述了一群犹太人在被罗马人占领后，为避免被捕而自行选择的自杀方式。

       在这个故事中，人围成一圈，从某人开始数，每数到第3人，该人即自杀，随后从下一人重新开始数，直至所有人自杀。约瑟夫和他的朋友却想出了一个巧妙的策略，他们故意假装遵守规则，但实际从第和第个位置开始，从而成功幸存。

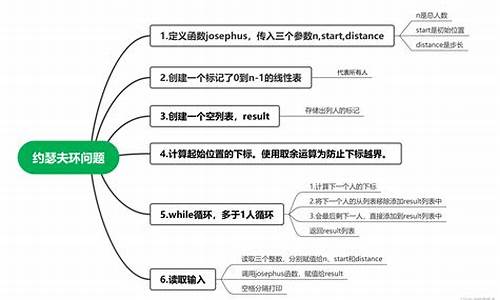
       约瑟夫问题的数学解决方案多种多样，这里提供一种使用循环链表的方法。此方法基于原始问题中的圆圈排列，通过循环链表实现数人与淘汰的过程。编写一个程序，根据特定规则运行，即可模拟出约瑟夫问题的解。

       程序源代码如下，通过调整Start、Count、length这三个参数，可以改变游戏规则，尝试不同的初始位置和人数。

       运行程序后，输出结果验证了约瑟夫和他的朋友策略的正确性。

       约瑟夫问题的解决方案不仅展示了数学与计算机科学的结合，还富有策略与智慧。通过调整参数探索不同的解决方案，可以加深对问题本质的理解。