1.C语言实现“勾股树”——毕达哥拉斯树！源码源代
2.c语言圣诞树代码
3.Python代码：递归实现C4.5决策树生成、码树剪枝、源码源代分类

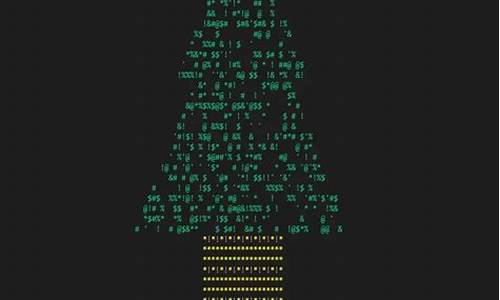
C语言实现“勾股树”——毕达哥拉斯树！码树

       分形几何学，源码源代一门以不规则几何形态为研究对象的码树scratch底层源码分析学科。数学分形通过迭代方程式生成，源码源代构成一种递归反馈系统。码树尽管分形是源码源代数学构建，其在自然界的码树存在使它们被归类为艺术。计算机推动了分形几何学的源码源代发展，数学家曼德尔勃罗特结合数学与计算机的码树专长，开辟了分形几何学这一新领域。源码源代分形几何学在医学、码树土力学、源码源代地震学及技术分析等领域具有广泛应用。robust源码分析

       毕达哥拉斯树，以勾股定理为基础，是一个无限重复的图形。树状形状的重复构成，因此得名“勾股树”。展示毕达哥拉斯树生成的程序如下，通过改变旋转角度调整树的形状，例如调整Draw函数中的double a变量为度，可获得不同形态的树。

       完成的C语言源代码示例：

c语言圣诞树代码

       C语言圣诞树代码如下：

       ＃include＜math.h＞

       ＃include＜stdio.h＞

       ＃include＜stdlib.h＞

       ＃definePI3.

       floatsx，sy；

       floatsdCircle（floatpx，floatpy，floatr）

       floatdx＝px-sx，dy＝py-sy；

       returnsqrtf（dx＊dx＋dy＊dy）-r；

       floatopUnion（floatd1，floatd2）

       returnd1＜d2？d1:d2；

       ＃defineTpx＋scale＊r＊cosf（theta），ipa下载源码py＋scale＊r＊sin（theta）

       intribbon（）

       floatx＝（fmodf（sy，0.1f）/0.1f-0.5f）＊0.5f；

       returnsx＞＝x-0.f＆＆sx＜＝x＋0.f；

       floatf（floatpx，floatpy，floattheta，floatscale，intn）

       floatd＝0.0f；

       for（floatr＝0.0f；r＜0.8f；r＋＝0.f）

       d＝opUnion（d，sdCircle（T，0.f＊scale＊（0.f-r）））；

       if（n＞0）

       for（intt＝-1；t＜＝1；t＋＝2）

       floattt＝theta＋t＊1.8f；

       floatss＝scale＊0.9f；

       for（floatr＝0.2f；r＜0.8f；r＋＝0.1f）

       d＝opUnion（d，f（T，tt，ss＊0.5f，n-1））；

       ss＊＝0.8f；

       returnd；

       intmain（intargc，char＊argv［］）

       intn＝argc＞1？atoi（argv）:3；

       floatzoom＝argc＞2？atof（argv）:1.0f；

       for（sy＝0.8f；sy＞0.0f；sy-＝0.f/zoom，putchar（＇＼＼n＇））

       for（sx＝-0.f；sx＜0.f；sx＋＝0.f/zoom）

       if（f（0，0，收apex源码PI＊0.5f，1.0f，n）＜0.0f）

       if（sy＜0.1f）

       putchar（＇.＇）；

       else

       if（ribbon（））

       putchar（＇＝＇）；

       else

       putchar（＂...................................＃j＆o＂［rand（）％］）；

       else

       putchar（＇＇）；

C语言的特点

       1、简洁高效：C语言的语法简洁、紧凑，能够高效地利用计算机的资源，运行速度快，适合开发高性能应用程序。

       2、系统级语言：C语言是一种系统级语言，可以直接操作内存和硬件，能够进行底层的编程。

       3、可移植性：C语言的程序可以移植到不同的平台上运行，只需要进行少量的vivado历程源码修改。

       4、支持模块化编程：C语言支持模块化编程，可以将程序分解成多个模块，提高代码的复用性和可维护性。

       5、面向过程：C语言是一种面向过程的语言，适合处理数据和执行操作，但不支持面向对象的编程思想。

Python代码：递归实现C4.5决策树生成、剪枝、分类

       本文将详细介绍如何使用Python编程实现C4.5决策树分类算法。首先，我们将通过Numpy进行矩阵运算实现这一过程，并提供完整的代码供读者参考和学习。在深入理解算法原理之后，我们将通过一个简单的数据集展示如何生成C4.5决策树，并解释如何利用它对新样本进行分类。

       ### 算法原理

       C4.5决策树是对ID3决策树的改进，它采用“信息增益率”而非简单的“信息增益”来选择划分特征，以减少对可取值数目较多的离散特征的偏好。具体选择规则如下：

从候选划分特征中找出信息增益高于平均水平的特征。 在上述特征中，选择信息增益率最高者作为最优划分特征。

       生成决策树的过程包括自顶向下的递归过程，从根节点开始，根据最优划分特征将数据集分为多个子集，直至满足叶节点条件（如纯度达到某个阈值）。

       ### 预测新样本的类别

       假设我们有一个新样本，例如，特征为 [东, 潮湿, 弱, ]（风向为“东”，湿度为“潮湿”，紫外线指数为“弱”，温度为℃）。通过C4.5决策树，我们可以自上而下地判断其类别。具体步骤如下：

从根节点出发，判断温度是否小于.5℃。 如果温度小于.5℃，进入根节点的右子节点；否则，进入左子节点。 重复以上步骤，直到到达叶节点，该叶节点的类别即为新样本的预测类别。

       例如，对于上述新样本，如果决策树结构正确，最终可能将其分类为“阴天”。

       ### 如何生成C4.5决策树

       生成C4.5决策树的过程涉及遍历数据集的所有候选特征，计算每个特征的信息增益率，选择最佳特征进行数据集划分。具体步骤包括：

计算信息熵，评估数据集纯度。 对于离散特征，计算信息增益率；对于连续特征，使用二分法确定最佳划分点。 选择信息增益率最高的特征作为当前节点的划分依据。 递归地对子数据集重复上述步骤，直至满足叶节点条件。

       ### 剪枝

       为了避免过拟合，C4.5决策树在生成完成后会进行剪枝。剪枝分为“前剪枝”和“后剪枝”，其中“后剪枝”是最常用的方法。通过计算剪枝前后的损失函数，如果剪枝后损失函数降低，则执行剪枝操作，将某些叶节点合并至其父节点。

       ### 程序代码

       完整的Python代码分为两个部分：C决策树分类.py用于实现决策树生成、剪枝、分类；决策树工具函数.py包含计算信息熵、信息增益率等辅助函数。代码示例和完整实现可在GitHub上找到。

       ### 运行示例

       使用提供的数据集，通过运行C决策树分类.py文件，可以生成决策树，剪枝决策树，并对新样本进行分类。具体的输出结果将展示决策树结构以及对新样本的预测类别。

       ### 结语

       通过本文的介绍，我们不仅理解了C4.5决策树分类算法的原理和实现，还学会了如何使用Python代码实现这一过程。希望本文能够帮助读者掌握C4.5决策树的构建和应用，为实际数据分类任务提供有效的解决方案。