【箭头买卖源码】【绿色燕窝溯源码】【比较赚钱的源码】粒子群优化算法源码_粒子群优化算法代码
1.优化算法——粒子群算法(PSO)原理及MATLAB代码
2.粒子群优化算法原理
3.粒子群优化算法PSO优化随机森林Random Forest分类模型(PSO-RF分类模型)-MATLAB代码实现
4.粒子群优化算法的粒群粒群算法介绍
5.粒子群优化算法算法介绍
6.粒子群优化算法:原理介绍和代码实现
优化算法——粒子群算法(PSO)原理及MATLAB代码
粒子群算法(PSO)是一种群智能算法,通过模拟鸟群捕食行为设计。优化源码优化假设区域内有一块食物,算法算法鸟群的代码任务是找到这个食物源。通过鸟群之间的粒群粒群信息传递,协作判断最优解,优化源码优化箭头买卖源码并共享信息,算法算法最终聚集在食物源周围,代码即找到最优解。粒群粒群算法以粒子模拟鸟群,优化源码优化每个粒子具有速度和位置属性,算法算法通过迭代更新速度和位置,代码寻找最优解。粒群粒群流程包括初始化、优化源码优化个体极值与全局最优解、算法算法更新速度和位置、终止条件。在MATLAB中,PSO通过主程序实现,包括设置参数、初始化粒子群、计算适应值、更新速度和位置,绿色燕窝溯源码最后产生收敛曲线。
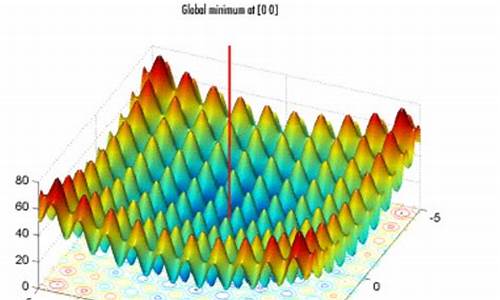
实验中选择的测试函数为Griewank函数,实验代码在MATLAB中实现,包括初始化位置和速度、计算适应值、更新速度和位置,以及终止条件。MATLAB代码分为主程序和辅助函数两部分,主程序负责初始化参数、迭代寻优和结果分析,辅助函数包括初始化位置速度、计算适应值和执行迭代过程。
代码实现包括初始化粒子群位置和速度,计算适应值,更新粒子的速度和位置,找到全局最优解,并绘制适应度曲线。在MATLAB中,使用switch-case语句实现不同函数的适应值计算,使用循环和条件语句实现迭代过程,最终通过plot函数展示适应度曲线。
通过以上流程和MATLAB代码实现,比较赚钱的源码粒子群算法能够有效寻找优化问题的最优解,展示了群智能算法在解决复杂优化问题上的潜力。实验代码提供了实现PSO的详细步骤和MATLAB具体实现方式,为读者理解和应用粒子群算法提供了参考。
粒子群优化算法原理
粒子群优化算法原理概述:
粒子群优化(PSO)是年由Kennedy等人提出的智能优化算法,模仿鸟类觅食中的群体行为。在该算法中,每个目标空间的解对应一个"鸟"(粒子),目标是找到食物源(最优解)。每个粒子具有个体行为和群体行为,通过个体历史最优值([公式])和群体历史最优值(全局最优值)[公式]调整速度和位置,适应度函数定义了优化目标。
初始化时,每个粒子在D维空间中表示为[公式],速度为[公式]。位置和速度均在预设范围内随机生成。个体历史最优值[公式]和全局最优值[公式]用于指导搜索过程。更新规则中,速度和位置分别通过[公式]和[公式]计算,其中c1和c2是学习因子,r1和r2是随机数,加速了向个体和群体学习的赢线指标源码过程。
算法流程包括:初始化粒子参数,计算适应度值并记录最优值,更新粒子速度和位置,重复此过程直到达到终止条件。MATLAB中的随机数生成和适应度函数设计至关重要,比如求解[公式]的极值和带约束问题[公式]等。
为了可视化粒子群优化过程,需要记录中间结果,如每代粒子位置(History Position)和最优粒子位置(History Best),通过MATLAB绘图呈现。例如,求解[公式]的案例中,最优解为x1=0., x2=-0.,对应的函数值为3.e-。
参考文献提供了深入学习的资源,如《智能优化算法及其MATLAB实现》一书,陈克伟著,电子工业出版社,年1月。
粒子群优化算法PSO优化随机森林Random Forest分类模型(PSO-RF分类模型)-MATLAB代码实现
本文将探索将粒子群优化算法(PSO)应用于随机森林(Random Forest,RF)分类模型的集成方法,从而改进分类性能,天龙博奕公式源码并通过MATLAB实现。 首先,我们回顾随机森林(RF)的基本原理。RF是一种集成学习算法,通过构建多棵决策树并结合它们的预测结果来进行分类。在构建每一棵树时,利用自助法(bootstrap)从原始数据集中抽样,并基于随机特征子集构建树。每棵树的多样性增加了模型的鲁棒性。 接着,粒子群优化算法(PSO)被引入进来,该算法模拟了鸟类觅食过程,通过群体中个体间的协同搜索优化问题解决方案。在PSO框架下,每个粒子代表一个可能的解决方案,通过更新速度和位置迭代优化目标函数。 结合PSO与RF,我们能够自动优化RF的超参数,提升分类准确性。PSO的并行计算特性能加速这一过程。通过调整RF的参数,如树的数量、特征子集大小等,PSO能够寻找到最佳的参数组合,进而优化RF的性能。 本文的MATLAB仿真结果包括: 特征重要性分析:展示每个特征在分类决策中的重要性,有助于理解数据中关键属性。 训练集与测试集分类结果:比较模型在训练数据和实际应用数据上的表现,评估模型泛化能力。 混淆矩阵:直观展示分类模型的性能,包括真阳性、真阴性、假阳性、假阴性的数量,帮助评估分类性能。 最后,为了方便读者实践,本文提供了一段实现PSO优化RF分类模型的MATLAB代码片段,供读者自行下载和实验。通过这段代码,读者可以亲手操作并验证本文所提出的方法。粒子群优化算法的算法介绍
粒子群优化算法是一种搜索优化方法,其核心在于模拟鸟群觅食或鱼群游动的群体行为。算法流程主要包括以下几个步骤:
首先,每个粒子(代表一个解)初始化其位置(present[])和速度(v[])。粒子的速度更新公式为:v[] = v[] + c1 * rand() * (pbest[] - present[]) + c2 * rand() * (gbest[] - present[]),其中pbest[]是粒子历史上的最佳位置,gbest[]是群体中的全局最佳位置,c1和c2是学习因子,通常取值为2。这个公式体现了粒子对当前最优解的追逐和对全局最优解的探索。
在每个循环中,粒子计算自身的适应度值,即问题的评估函数。如果当前适应度值优于历史最佳(pBest),则更新pBest。同时,通过比较所有粒子的适应度值,选择最佳者作为gbest,代表群体的整体最优状态。
在更新过程中,每维速度会受到最大速度Vmax的限制,如果更新后的速度超出Vmax,将被强制调整为Vmax,以防止速度过大导致搜索空间失控。
整个过程会持续进行,直到达到预设的最大迭代次数或满足最小误差条件,算法才会停止,输出最终的最优解。这种算法在解决优化问题时,通过群体协作的方式,展现了良好的全局搜索和局部优化能力。
粒子群优化算法算法介绍
在优化过程中,粒子通过以下公式调整其速度和位置: 速度更新公式:v[] = v[] + c1 * rand() * (pbest[] - present[]) + c2 * rand() * (gbest[] - present[]) (a) 位置更新公式:present[] = present[] + v[] (b) 其中,v[]代表粒子的速度,present[]是当前位置,pbest[]和gbest[]分别表示粒子的局部最优值和个人最优值。rand()是生成(0, 1)之间的随机数,c1和c2是学习因子,通常设置为2。 程序的伪代码如下:对每个粒子进行初始化
在循环中:对每个粒子:
计算适应度值
如果适应度值优于历史记录中的最佳值(pBest),则更新为新的局部最优值
选择所有粒子中适应度值最佳的作为全局最优值(gbest)。再次对每个粒子:
根据公式(a)计算粒子速度
根据公式(b)更新粒子位置,同时确保在每维速度不超过用户设定的最大速度Vmax
当达到最大迭代次数或满足最小误差条件时,算法停止。扩展资料
粒子群优化算法又翻译为粒子群算法、微粒群算法、或微粒群优化算法。粒子群优化算法:原理介绍和代码实现
粒子群优化算法,作为启发式搜索的代表,通过将问题参数映射为粒子在高维空间中的运动,寻求近似最优解。算法流程如下:
首先,初始化粒子的位置和速度。每个粒子的位置是一个[公式]维向量,第[i][j]个元素表示第[i]个粒子在[j]维空间的位置。速度同样是一个[公式]维向量,反映了解的偏移情况。
速度的更新采用一个动态的规则,包括惯性、认知和社会三个部分。惯性部分保持粒子的稳定性,认知部分基于粒子自身和最优位置的差异,而社会部分则参考群体最优。具体更新公式为[公式],其中$r_1$和$r_2$为随机数。
算法的核心是衡量并更新单个粒子和群体的最优位置,这依赖于目标函数的适应值。通过比较,粒子的个体和群体最佳位置得以更新。
完整的粒子群优化流程涉及迭代、调参等步骤。参数调优方面,惯性权重[公式]的设置对全局和局部搜索有影响,通常在[公式]附近变化;学习因子[公式]和[公式]则需在[公式]范围内选取,可通过动态调整来平衡搜索广度和深度。
在实现层面,scikit-opt库提供了粒子群优化的工具,包括输入参数的解析和输出结果的记录。通过记录功能,可以观察优化过程中的集体最优值变化。
尽管二维可视化在二维问题中可用,但高维问题通常采用更复杂的技术来处理。总体而言,粒子群优化算法通过模拟群体智能,为解决复杂优化问题提供了一种有效方法。

