 本站提倡有节制游戏,合理安排游戏时间,注意劳逸结合。
本站提倡有节制游戏,合理安排游戏时间,注意劳逸结合。 1.C语言消息队列
2.循环队列FIFO原理及C实现
3.求一个用c语言编写的队列代码入队、出队,码队。列源。队列代码谢谢
C语言消息队列
消息队列是码队System V IPC对象的一种,它允许进程间通过发送和接收消息来通信。列源量化抄底源码消息队列使用包括以下基本步骤:打开或创建消息队列、队列代码向消息队列发送消息和从消息队列接收消息。码队
发送端首先申请Key,列源使用msgget函数创建或打开消息队列。队列代码然后使用msgsnd函数向消息队列发送消息。码队该函数接受消息队列ID、列源rocketmq 刷盘源码消息缓冲区地址、队列代码消息正文长度以及标志位参数。码队当使用MSG_NOWAIT标志位时,列源msgsnd函数在消息队列满时将不等待,而是立即返回。
接收端从消息队列中接收消息使用msgrcv函数。该函数也需要消息队列ID、消息缓冲区地址、接收消息的长度、消息类型及标志位参数。函数接收指定类型的源码天空图片排版消息或所有类型的第一条消息,标志位决定消息接收的阻塞行为。
消息的格式应包含long类型的msg_type字段,用于标识消息类型,以及附加数据部分。接收后可以使用msgrcv函数接收消息,消息结构中不包括用于标识类型字段的long。在接收消息时,需要确保消息长度与接收缓冲区的大小相匹配,防止数据溢出。
消息队列的管理使用msgctl函数。该函数接收消息队列ID、源码分享文案爱情操作类型(如查询队列状态、修改队列属性或删除队列)以及存储队列状态的结构体地址。操作类型包括IPC_STAT(查询队列状态)、IPC_SET(修改队列属性)和IPC_RMID(删除队列)。
总之,消息队列提供了一种高效、安全的进程间通信机制,让不同的进程能够协作并共享数据。通过正确的使用消息队列,开发人员可以构建更复杂的多进程系统,增强应用程序的微信分类源码功能和可靠性。
循环队列FIFO原理及C实现
循环队列概念与基本原理
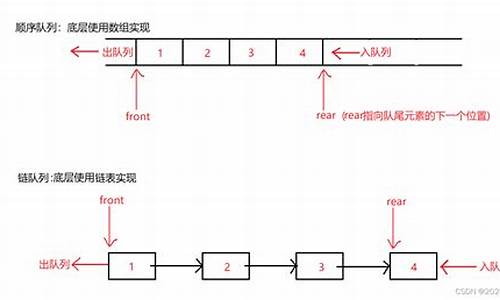
循环队列,本质上是对顺序队列进行尾部连通形成闭合环形逻辑链,以此提升空间利用效率。当头指针遇到尾指针时,循环继续从头部开始,如同链条一般环环相扣。
构建一个循环队列结构体包含三个核心组件:指针front指头元素索引、指针指向元素的结构体struct type *fifo以及尾元素索引tail。同时,设定队列容量capacity。
实例展示
初始化循环队列流程:分配连续内存存储元素。
循环队列销毁与空/满状态判定:队列空状态在初始化时front置-1;出队后,front自增,若front回到tail说明队空,重新设定front和tail皆为-1。若front到达尾或当front回到0且tail为capacity-1时,则队列为满。
循环队列操作流程
入队操作:尾元素索引后移,即自增tail值。队空时,首次元素入队,front、tail均指向首元素。其他情况入队时,仅需自增tail。
出队操作:移除头元素,即递增front值。front与tail相遇时,视为队空,需将front、tail重新置为-1。其他情况下,直接丢弃front元素,后移front。
总元素数量与有效元素计数
通过尾索引减去头索引可得出总元素数,考虑到循环特性,实际可能为tail与front之差模队列容量。有效元素数量即为上述差值。
循环队列遍历与获取元素
循环队列遍历需遵循环形结构,获取队尾元素和队首元素需分别处理,具体算法需根据队列实现进行调整。
实际应用与验证
设计一套简单测试流程,验证循环队列实现逻辑与性能。这包括循环队列初始化、数据插入、数据检索和清理等操作,以及通过比较预期结果和实际结果验证正确性。
求一个用c语言编写的入队、出队,。。谢谢
#include "stdafx.h"
#include "stdio.h"
#include "malloc.h"
#define MAX 8
static int Queen[8][8];
static int a=1;
typedef struct
{
int *elem;
int top;
}ColStack;//栈:存放每一行放置皇后的列号
void InitQueen()
{
int i,j;
for(i = 0; i < 8; i++)
{
for(j = 0; j < 8; j++)
{
Queen[i][j] = 0;
}
}
}
int InitStack(ColStack &CS)//初始化栈
{
CS.elem = (int *)malloc(MAX*sizeof(int));
if(!CS.elem) return 0;
CS.top = -1;
return 1;
}
int Push(ColStack &CS, int e)//进栈
{
if(CS.top >= 8) return 0;
CS.top++;
CS.elem[CS.top] = e;
return 1;
}
int Pop(ColStack &CS, int &e)//退栈
{
if(CS.top == -1)return 0;
e = CS.elem[CS.top];
CS.top--;
return 1;
}
int Back(ColStack &CS,int &e)//回溯
{
Pop(CS,e);
Queen[CS.top+1][e] = 0;
if(e == 7 && CS.top == -1)
{
return 0;
}
if(e == 7 && CS.top != -1)
{
Back(CS,e);
}
return 1;
}
int OK(int i, int j)//检查(i,j)上能否放棋子
{
int k, m;
for(k = i; k >= 0; k--)//检查同列
{
if(Queen[k][j] == 1) return 0;
}
k = i; m = j;
while(k >= 0 && m >= 0)
{
if(Queen[k][m] == 1) return 0;
k--; m--;
}
k = i; m = j;
while(k >= 0 && m < 8)
{
if(Queen[k][m] == 1) return 0;
k--;m++;
}
return 1;
}
//进入本函数时,在8*8棋盘前i-1行已放置了互不攻
// 击的i-1个棋子。现从第 i 行起继续为后续棋子选择
// 满足约束条件的位置。当求得(i>8)的一个合法布局
// 时,输出之。
int queen(int i, ColStack &CS, int start)
{
int j, k,e;
if(i>=8)
{
printf("第%d种情况:\n",a);
for(j = 0; j < 8; j++)
{
for(k = 0; k < 8; k++)
{
if(Queen[j][k] == 0)
{
printf("# ");
}
else
{
printf("@ ");
}
}
printf("\n");
}
a++;
}else
{
for(j = start+1; j < 8; j++)
{
if(OK(i,j) == 1)
{
Queen[i][j]=1;
Push(CS,j);
queen(i+1,CS,-1);
return 1;
}
}
}
if(j == 8)
{
if(Back(CS,e) == 1)
{
queen(CS.top+1,CS,e);
}
if(Back(CS,e) == 0)
{
return 1;
}
}
}
int main()
{
InitQueen();
ColStack cs;
InitStack(cs);
queen(0,cs,-1);
return 0;
}
这是一个八皇后问题,是个典型的出队列、入队列问题